As X Increases Y Decreases / Brush up your maths: answer to straight line graphs exercise / As x decreases, y decreases c.

As X Increases Y Decreases / Brush up your maths: answer to straight line graphs exercise / As x decreases, y decreases c.. Which statement correctly describes the linear function, y=10x + 5? For more details, go through the upcoming sections. The answer you are looking for is as x increases, y decreases then increases. As x increases in value, does y increase or decrease? For a decreasing function y decreases as x increases and thus change in y.

A) as x increases by 1, y increases by 5. In other words, for increasing the units by one, the time minutes increases by 15.509, while there is 4.162 minutes does not depend on the unites. A function is decreasing, if as x increases (reading from left to right), y decreases. As you can see from the above figure that at the right of the origin, the curve is moving upwards as. In the case of as x increases and y also increases or in the statements as x decreases and y decreases this exhibits a direct, proportional or linear relationship.

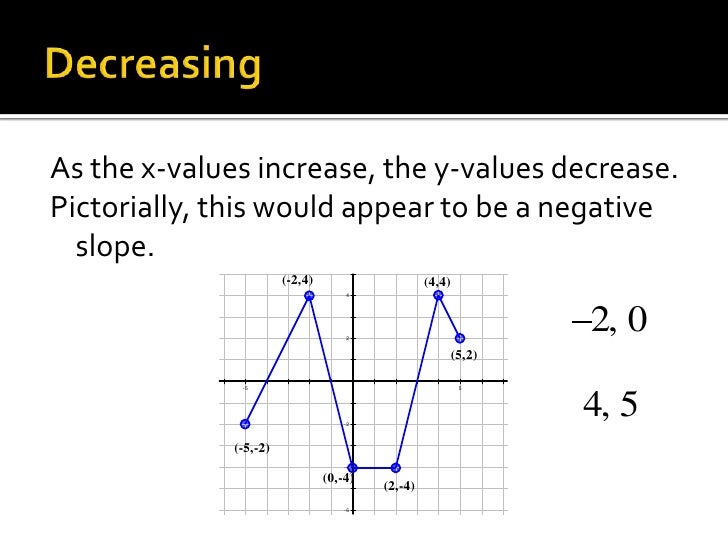
Interval notation from image.slidesharecdn.com

Y varies directly to some quantities and varies inversely to some other quantities. The ratio is the slope of the line, which in calculus is a derivative. As x increases, y decreases, and at an increasing rate. Y = kx inverse variation: The answer you are looking for is as x increases, y decreases then increases. In other words, for increasing the units by one, the time minutes increases by 15.509, while there is 4.162 minutes does not depend on the unites. This function remains positive during the limiting process and therefore f'(x)>0. This always occurs at the points where a function changes from increasing to decreasing and at the points where a function.

When it is increased to 2, the value of y decreases.

Also, if x decreases, then y increases by k. This means that whenever x increases, y decreases and it decreases by k times as much as the increase in x. As you can see from the above figure that at the right of the origin, the curve is moving upwards as. This always occurs at the points where a function changes from increasing to decreasing and at the points where a function. However, if y falls as x increses, you have a negative correlation. The values of y either remain constant, increase or decrease. This function remains positive during the limiting process and therefore f'(x)>0. As x increases, y also increases 2. When x1 < x2 then f(x1) ≥ f(x2). As x increases, y decreases, and at an increasing rate. Is increasing and where it is decreasing is. As x increases, y increases and then decreases. Y = kx inverse variation:

F(x) = x3−4x, for x in the interval −1,2. Into the derivative to determine if the function is increasing or decreasing. This function remains positive during the limiting process and therefore f'(x)>0. O as x increases, y decreases and then increases. The answer you are looking for is as x increases, y decreases then increases.

D X causes Y If Y decreases as X increases then X must ... from www.coursehero.com

Y = kx inverse variation: When it is increased to 2, clearly the now observe the values of y when x is negative 1. This site will be using open interval notation to represent intervals of increasing and decreasing. As x increases, y decreases, and at an increasing rate. As x decreases, y also decreases. For a function y=f(x) : As x increases, y increases and then decreases. I will give you three simple examples.

That's why we are also come up with the new calculator ie., what is the percentage increase/decrease from x to y.

For a function y=f(x) : O as x increases, y decreases and then increases. As x increases, y also increases 2. Start studying increasing and decreasing functions. As variable x increases, variable z decreases. For more details, go through the upcoming sections. A) as x increases by 1, y increases by 5. For a decreasing function y decreases as x increases and thus change in y. As x decreases, y decreases c. I think it is possible to make these sentences unambiguous by specifying whether y is increasing or decreasing explicitly after with. It looks like a steady decrease but i was thinking more of a negative exponent? As x increases y increases but at a decreasing rate as x increases, y increases, but at a decreasing rate. However, if y falls as x increses, you have a negative correlation.

Since r is negative, as x increases, y decreases. If y increases as x increases, you are referring to a positive correlation. A function is decreasing, if as x increases (reading from left to right), y decreases. As x increases, y also increases 2. As x increases, y decreases, or as y increases, x decreases.

Solved: Which Of The Following Statements Is Correct? Mult ... from media.cheggcdn.com

For a decreasing function y decreases as x increases and thus change in y. That is, it is decreasing if as x increases, y decreases. Which statement correctly describes the linear function, y=10x + 5? Ask your teacher which notation convention is preferred in your classroom. O as x increases, y decreases and then increases. Usually, students calculate percent increase and percent decrease by using the percent change formula or direct formulas earlier. Here we introduce these basic properties of functions. Since r is negative, as x increases, y decreases.

6 this scatterplot displays the association between the hours of training a person has and the number of mistakes that person makes on a particular task.

Y varies directly to two or more quantities 5. This function remains positive during the limiting process and therefore f'(x)>0. Ask your teacher which notation convention is preferred in your classroom. We can say that as increases, is increasing faster than , and is increasing faster than the increase in. O as x increases, y decreases and then increases. This always occurs at the points where a function changes from increasing to decreasing and at the points where a function. It looks like a steady decrease but i was thinking more of a negative exponent? Usually, students calculate percent increase and percent decrease by using the percent change formula or direct formulas earlier. In other words, for increasing the units by one, the time minutes increases by 15.509, while there is 4.162 minutes does not depend on the unites. F(x) = x3−4x, for x in the interval −1,2. If it increases everything would go farther away from us and if it would decrease galaxies and planets would come. Start studying increasing and decreasing functions. If the ratio is negative, x increasing makes y decrease.

Cari Blog Ini

elrincondexo

Unggulan

Stuck In The Wall Gril - The Girl That Got Stuck in the Wall - Chapter 1 - At least, until one day when he takes a wrong turn down an alley and discovers jieun… stuck in a wall.